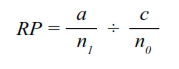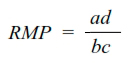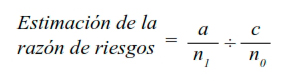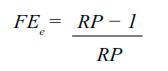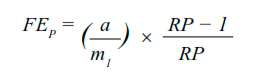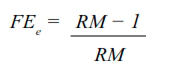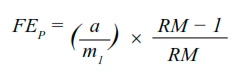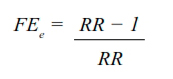METODOLOGÍA DE LA INVESTIGACIÓN

Medición en epidemiología: prevalencia, incidencia, riesgo, medidas de impacto

Measurement in epidemiology: prevalence, incidence, risk, impact measures

Arturo Fajardo-Gutiérrez¹

¹Instituto Mexicano del Seguro Social, Centro Médico Nacional Siglo XXI, Hospital de Pediatría, Unidad de Investigación en Epidemiología Clínica. Ciudad de México, México

Este artículo debe citarse como: Fajardo-Gutiérrez A. Medición en epidemiología: prevalencia, incidencia, riesgo, medidas de impacto. Rev Alerg Mex. 2017;64(1):109-120

Resumen

En epidemiología es primordial la medición, por ello es necesario un conocimiento detallado de las diferentes medidas que se estiman en esta disciplina, porque de esto depende la interpretación de la información y, lo más importante, las decisiones que se tomen en la atención de los pacientes. En este artículo se describen los tres principales grupos de medidas en epidemiología: frecuencia, asociación e impacto potencial; se dan ejemplos y se indica cómo deben calcularse. La incidencia y la prevalencia son las medidas de frecuencia más significativas y pueden obtenerse cuando se estudia la morbilidad y mortalidad de las enfermedades; en la epidemiología descriptiva son fundamentales e implican estudiar cómo se distribuye la enfermedad en la población, en particular, la incidencia según la persona, lugar y el tiempo. También se detallan las medidas de asociación que se emplean en la epidemiología analítica, como la razón de prevalencias, razón de momios y el riesgo relativo. Además, se abordan el riesgo atribuible, las fracciones poblacionales y etiológicas en expuestos y las medidas de impacto potencial. En general es importante considerar que la pertinencia de calcular las medidas de frecuencia, de asociación y de impacto potencial depende del diseño de estudio.

Palabras lave: Estudios epidemiológicos; Incidencia; Prevalencia; Medidas de asociación; Medidas de impacto potencial

How to cite this article: Fajardo-Gutiérrez A. Measurement in epidemiology: prevalence, incidence, risk, impact measures. Rev Alerg Mex. 2017 Jan-Mar;64(1):109-120

Abstract

Measurement is essential in epidemiology, and this is why detailed knowledge of the different measures that are estimated in this discipline is necessary, since information interpretation and, most importantly, the decisions made in the care of patients depend on it. This article describes the three main groups of measures in epidemiology: frequency, association and potential impact; examples and instructions for their calculation are also provided. Incidence and prevalence are the most significant frequency measures, and can be obtained when both morbidity and mortality of diseases are studied. In descriptive epidemiology these measures are fundamental and involve studying how the disease is distributed in the population, in particular, the incidence according to the individual, place and time. The measures of association that are used in analytical epidemiology, such as prevalence ratio, odds ratio and relative risk, are also detailed. In addition, attributable risk, population and etiological fractions of exposed subjects and measures of potential impact are addressed. In general, it is important to consider that the relevance of calculating the frequency, association and potential impact measures depends on the study design.

Keywords: Epidemiological studies; Incidence; Prevalence; Measures of association; Measures of potential impact

Abreviaturas y siglas

DI, densidad de incidencia

DR, diferencia de riesgo

IA, incidencia acumulada

IIH, infecciones intrahospitalarias

P, prevalencia

RM, razón de momios

RMP, razón de momios de la prevalencia

RP, razón de prevalencia

t, tiempo

T/O, traumatología/ortopedia

TP, tiempo-persona exposición

Antecedentes

La medición de los diferentes indicadores que se estudian en la epidemiología es vital en el estudio de las enfermedades en la población. Deben conocerse con suficiente detalle, porque de la forma como se obtienen se derivarán las conclusiones a las que se llegue y, lo más importante, inclinarán a tomar alguna decisión en la atención médica de los pacientes o de una población, con el consiguiente daño o beneficio inherente a su adecuada interpretación.

La epidemiología tiene diferentes definiciones y una de las más conocidas es la siguiente:

Es la rama de la medicina que estudia la distribución de las enfermedades en la población y sus determinantes.

En esta definición se señala toda su metodología; por una parte, describir la distribución de la enfermedad en la población mediante el estudio de la incidencia (que dicho sea de paso es la “medida reina” de los estudios epidemiológicos) y establecer cómo se distribuye la incidencia según el sexo, la edad, la raza y otras variables ―no tan fáciles de medir― como el estrato social o, incluso, conocer la incidencia según la residencia (urbana/rural), todo lo cual se conoce como epidemiología descriptiva.

El resultado de estos conocimientos puede apoyar a establecer hipótesis etiológicas que dirigirán el segundo gran rubro del quehacer de la epidemiología: determinar las causas (causalidad) de las enfermedades en una población, lo cual se ha denominado epidemiología analítica.

Antes del estudio de la distribución de las enfermedades en la población debe conocerse que:

• Razón = A/B. Integrada por dos componentes (A y B), el numerador no está incluido en el denominador, por ejemplo, la razón masculino/femenino.
• Proporción = A/A + B. Tiene dos componentes (A y A + B), donde el numerador está incluido en el denominador, por ejemplo, las leucemias representan 40 % del total los cánceres en los niños. Es adimensional y sus valores se encuentran entre 0 y 1.
• Tasa = A/A + B · t. Tiene 3 componentes (A, A + B y t, tiempo), por ejemplo, la incidencia de cáncer en los niños mexicanos es de 0.000124 niños/año (124 × 1 000 000 niños/año).

La medición en epidemiología puede llevarse a cabo estudiando a las personas que enferman, es decir, analizando la morbilidad de o por las enfermedades; cuando el objetivo son las personas que fallecen, se estudia la mortalidad de las enfermedades.

Medidas de frecuencia

El estudio de las medidas de frecuencia, tanto en la morbilidad o mortalidad, comprende el análisis de la incidencia y prevalencia.

Incidencia

Comúnmente denominamos solo como incidencia a la tasa de incidencia, dado que el concepto tasa va implícito. La principal propiedad de esta medida es determinar los casos nuevos que se presentan en una población en un tiempo determinado, de ahí que para su cálculo se requiere un periodo de seguimiento. En forma general se conocen dos tipos de incidencia:

1. Incidencia acumulada

Esta medida cumple con el requisito de una tasa, es decir, tiene 3 componentes: numerador = A, denominador = A + B y t = tiempo. Generalmente para obtener esta medida se necesita tener un grupo de individuos que no tengan la enfermedad que se estudia, algunos de los cuales después de un tiempo determinado (por ejemplo, meses o años) pasan del estado de salud al de enfermedad. En esta medida, el numerador lo constituyen los individuos que enfermaron (A) y el denominador, los que no lo hicieron (A + B).

Por último, en este tipo de incidencia el tiempo (t) es fijo para todos los individuos, es decir, independientemente del momento en que enfermaron, todos tuvieron el mismo tiempo de seguimiento; por ello, el tiempo se elimina de la ecuación y solo queda A/AB.

La forma de analizar una tasa de incidencia acumulada (IA) es como una proporción, la cual puede multiplicarse por 100. Para ejemplificar: si se ha realizado el seguimiento a 100 individuos sanos durante un mes y se enfermaron 20, entonces se tendría que la IA en un mes fue de 20 % (IA = 20/100; IA = 0.2 × 100; IA = 20 %).

El tiempo de no exposición en los individuos que enferman es variable en esta tasa de incidencia y depende del momento en que enferman durante el periodo de estudio, situación que debería descontarse del tiempo total de seguimiento, sin embargo, no se toma en cuenta para el cálculo final.

2. Densidad de incidencia (DI)

Con esta medida se busca resolver el problema señalado para la IA; el cambio fundamental estriba en contabilizar el tiempo de exposición de toda la cohorte de estudio. Para esto existen dos métodos:

• Sumatoria del tiempo/persona exposición de la cohorte de estudio. En este método, el denominador se estima sumando el tiempo de exposición sin la enfermedad en todos los individuos. Se infiere que solo sucede en los individuos que enferman, porque los individuos que no enferman tienen todo el tiempo de exposición del periodo de estudio. Es decir, si una cohorte de individuos sanos es seguida para conocer en cuánto tiempo enferman, el tiempo de riesgo de exposición se mide hasta que el individuo enferma, después de que lo hace ya no se agrega tiempo de exposición. Este aspecto se comprende mejor en el ejemplo que se grafica en la Figura 1: 6 individuos que ingresaron a un estudio en diferente momento y de quienes se conoció el tiempo de exposición hasta que desarrollaron la enfermedad, abandonaron el estudio o se terminó la investigación. Los rombos representan las pérdidas de seguimiento (2 casos, E y A) y los círculos, a los individuos que enfermaron (2 casos: B y D); los otros dos individuos (C y F) completaron el periodo de 12 meses de seguimiento sin enfermar.
  
  

  Figura 1. Tiempo-persona de una cohorte de 6 individuos. (Modificado de Abraira V. Medidas de frecuencia de la enfermedad)

  
  Para determinar de manera más sencilla el tiempo-persona exposición (TP) se coloca a los individuos como si todos iniciaran al mismo tiempo, como se observa en la Figura 2.
  
  

  Figura 2. Tiempo-persona de una cohorte de 6 individuos. Se coloca a todos como si todos iniciaran al mismo tiempo (Modificado de Abraira V. Medidas de frecuencia de la enfermedad)

  
  Lo que podemos observar es que los individuos del rombo rojo se perdieron de la cohorte, los del círculo azul desarrollan la enfermedad. Así, los individuos A y E tuvieron 3 y 5 meses de TP, los individuos B y D tuvieron 3 y 8 TP y los individuos C y F, 12 meses de TP cada uno. En forma global se obtiene un total de 3 + 3 + 12 + 8 + 5 + 12 = 43 meses de exposición (TP), por lo tanto, el cálculo de la DI es:
  
  DI = 2/43 (2 representan a quienes enfermaron) = 0.0465 × 1000, cuyo resultado expresa 46.5 casos por 1000 meses-persona
  
  Este método puede aplicarse cuando la cohorte de individuos es pequeña, porque en la medida en que la cohorte aumenta se vuelve más difícil calcular o estimar el TP.

• TP cuando la cohorte es grande. Cuando se tienen más de 100 individuos, el TP se puede obtener multiplicando el número de individuos por el tiempo de seguimiento. Por ejemplo, si se tiene una cohorte de 100 individuos y se siguen por espacio de dos meses se tendría:
  
  TP = 100 × 2 = 200 (meses/persona)
  
  Pero si el seguimiento es por dos años, entonces tendríamos:
  
  TP = 100 × 2 = 200 (años/persona).
  
  En este ejemplo, solo la unidad de medida es diferente: en el primer caso son meses/persona y en el segundo años/persona.
  En poblaciones grandes (más de 1000 personas) es común que se obtenga la tasa anual dividiendo el número de casos registrados durante el año entre el total de personas estimadas. Generalmente, la estimación de poblaciones se realiza al 30 de junio del año en curso. A las tasas anual también se les conoce como tasas ordinarias, generales o comunes; se calculan conociendo el número de personas que enfermaron por determinada enfermedad entre la estimación de la población.
  Debe señalarse que tanto para la IA y la DI, la unidad de tiempo (sean meses o años en el denominador) son iguales. Es decir, el riesgo (IA) y la tasa (DI) son iguales a la unidad (cuando el denominador es un mes o un año de seguimiento); así, cuando una cohorte de personas se sigue durante un mes, la IA y DI son iguales; cuando el seguimiento es a un año, nuevamente tanto la IA y DI serán iguales. De lo anterior se desprende que tanto el riesgo (individual) como la tasa (riesgo poblacional) son iguales cuando el tiempo de seguimiento es 1 (sea un mes o un año).
  Comprender la importancia de la DI, así como la diferencia entre la IA y DI no es fácil, por ello se propone un ejercicio.

Con los resultados del ejercicio observamos como la IA (debido a que el tiempo es fijo para todos los pacientes) no distingue en qué servicio hay mayor riesgo de desarrollar una IIH. En cambio, cuando calculamos la DI se puede determinar que el riesgo de enfermar es mayor en el servicio de urgencias (0.1 comparado con 0.02), lo cual se comprueba con el riesgo relativo (RR) = 5. Se concluye que en el servicio de urgencias se tiene un riesgo mayor de desarrollar una IIH por lo cual sería más conveniente iniciar el programa de lavado de manos en él, dado que la velocidad con la que se enferman los pacientes es mucho más rápida que en el servicio de T/O.

Prevalencia

Como se señaló, la prevalencia es una proporción (P = A/A+B) y aunque también se le denomina como tasa de prevalencia, en realidad no lo es porque falta el tiempo, por ello también se le conoce como pseudotasa. La prevalencia mide la proporción de personas que se encuentran enfermas al momento de evaluar el padecimiento en la población, por lo tanto, no hay tiempo de seguimiento. Existen dos tipos de prevalencias:

• Prevalencia puntual. Esta prevalencia es la más común y, como un ejemplo podría conocerse el número de individuos internados en un hospital por un cuadro agudo de asma; aquí el número de pacientes internados por un cuadro agudo de asma es el numerador, mientras que el denominador será el total de pacientes internados en el hospital respectivo.
• Prevalencia de periodo. La prevalencia de periodo se define como la frecuencia de una enfermedad en un periodo de tiempo. Es una proporción que expresa la probabilidad que un individuo sea un caso en cualquier momento dentro de un determinado periodo de tiempo. El numerador serán los casos que desarrollaron la enfermedad antes y durante el periodo de estudio y el denominador es la población durante todo el periodo de estudio. El principal problema que plantea el cálculo de este índice es que la población total puede cambiar durante el período. Normalmente la población que se toma como denominador corresponde al punto medio del período considerado.

Cabe comentar que cuando se señala la prevalencia sin ninguna especificación de un tiempo durante el periodo de estudio, se está calculando prevalencia puntual.

Por último, es necesario conocer la relación que guardan la prevalencia, la incidencia y la duración promedio de la enfermedad. La fórmula de la prevalencia es:

Donde:

P = Prevalencia de la enfermedad

I = Incidencia
__
T = Duración promedio de la enfermedad

Es decir, la prevalencia aumentará, disminuirá o será estable dependiendo de la incidencia y la duración promedio de la enfermedad. Como ejemplo, utilizamos la prevalencia de los niños con cáncer, en quienes la prevalencia se ha incrementado porque la duración promedio de la enfermedad ha aumentado a pesar de que su incidencia es estable.

Para finalizar, en el Cuadro 1 se sintetiza los atributos y unidades de medición de la IA, DI y prevalencia.

Tendencia de la incidencia

Debemos puntualizar que en la epidemiología descriptiva de cualquier enfermedad el objetivo es conocer cómo se distribuye la enfermedad en la población, por ello lo primero que tenemos que estudiar son 3 características de la distribución de las enfermedades:

• Incidencia según la persona.
• Incidencia según el lugar de residencia.
• Incidencia según el tiempo.

En el siguiente texto se resumen estos 3 elementos:

• Incidencia de cáncer en los niños (0 a 14 años) derechohabientes del IMSS residentes de cinco estados de la República Mexicana durante el periodo de 1996 a 2013.

En el enunciado anterior se señala que se presenta el riesgo poblacional (incidencia) de cáncer en niños, de determinado lugar (cinco estados de la República Mexicana) y durante un periodo de 18 años (periodo de 1996 a 2013).

Pero cuando se quiere ser explícito sobre la tendencia de la incidencia, o sea si ha existido algún aumento, disminución o estabilidad en el riesgo poblacional, se deben considerar algunas características como la tendencia de una enfermedad, es decir, el incremento, decremento o estabilidad deben señalarse calculando la tasa. En el ejemplo anterior, si decimos que en el periodo de 1996-2013 tuvimos una tendencia de casos al aumento, no podemos afirmar que el riesgo de desarrollar la enfermedad en estudio está aumentando en la población; para determinar lo anterior debe calcularse la tasa de incidencia. El mayor número de casos solo indica que el denominador pudo aumentar y por eso tenemos más casos, pero no podemos señalar que el riesgo de desarrollar la enfermedad se ha incrementado.

Por ello, cuando presentamos la tendencia de las tasas en determinado periodo (1996 a 2013) y observamos que con el tiempo la incidencia va en aumento, debe interpretarse que el riesgo de desarrollar la enfermedad en la población de estudio va en aumento y, por lógica, debemos estudiar las causas de esa tendencia, de igual forma si la tendencia de la incidencia disminuye. Una tendencia de la incidencia estable indica que el riesgo de desarrollar la enfermedad no ha aumentado.

Para calcular la tendencia de una enfermedad debe tenerse un registro del número de casos que se presentan en la población cada año. Con los datos recabados se obtendrá el numerador de la tasa anual, el cual se dividirá en la población en riesgo para el año de estudio.

A este tipo de tasa de incidencia se les conoce como tasa de incidencia ordinaria, para obtenerla se divide el número de casos en un año específico (numerador) entre la población estimada al 30 de junio del año en estudio (denominador). Si estamos analizando el periodo de 1996 a 2013, la incidencia para cada año será el número de casos registrados por cada año entre la población estimada para ese año. Pero si quisiéramos conocer la incidencia promedio que se tuvo durante el periodo de 1996 a 2013, se deberá sumar el número de casos registrados durante el periodo de 18 años y, si la población ha sido estable, el denominador lo conformará la población estimada para el primer año de estudio (en 1996) y dado que la población permaneció estable esta población se multiplicará por 18, años de duración del periodo bajo escrutinio. Si la población no ha sido estable, sino que ha disminuido o incrementado, se deberán sumar las poblaciones registradas o estimadas para los años del periodo, que en el ejemplo serían 18 (1996 a 2013).

Finalmente se debe recordar que la tendencia de una enfermedad debe estimarse calculando las tasas, no solo señalando el número de casos absolutos.

Medidas de asociación

Las medidas de asociación básicas dependen del estudio que se realice y las principales son:

• Razón de prevalencia.
• Razón de momios de la prevalencia.

Estas medidas se obtienen cuando se lleva a cabo un estudio transversal analítico (Figura 3), cuya característica principal es obtener una muestra aleatoria y probabilística de la población de estudio. El objetivo es conocer la prevalencia de la enfermedad y buscar los factores asociados.

Figura 3. Esquemas conceptuales de diseño y análisis para un estudio transversal analítico

Debido a que tanto la enfermedad como los factores de riesgo que se analizan se miden en el momento de la investigación, uno de los principales problemas con este diseño es que las asociaciones encontradas pudieran tener ambigüedad temporal, es decir, debido a que no hay seguridad de que la exposición al factor de estudio fue antes de la enfermedad, aunque se haya encontrado alguna asociación, no puede establecerse como tal; todos los marginales fluctúan aleatoriamente. De ahí que con frecuencia estos estudios se utilicen como exploratorios, para investigar en forma global el o los posibles factores de exposición que podrían influir en el desarrollo de alguna enfermedad.

Razón de prevalencia (RP)

La RP se obtiene mediante la siguiente ecuación:

Esta medida de asociación se obtiene cuando la enfermedad que se estudia tiene un periodo de desarrollo o exposición conocido, lo cual ocurre en las enfermedades infecciosas.

Razón de momios de la prevalencia (RMP)

La RMP se obtiene mediante la siguiente ecuación:

Esta medida de asociación se obtiene cuando la enfermedad que se estudia no tiene o se desconoce el periodo de exposición para producir la enfermedad, peculiaridad que se observa en las enfermedades crónicas.

Es importante señalar que la forma como se interpretan las medidas de asociación siempre será dependiente de la escala, factor que se ejemplifica en la Figura 4.

Figura 4. Escala para la interpretación de las medidas de asociación

1. Razón de momios (odds ratio)

Esta medida se obtiene de un diseño de casos y controles (Figura 5), en el que los casos son los individuos enfermos que se comparan con individuos no enfermos o que no tienen la enfermedad investigada. Debe recordarse que los casos deben ser representativos de las personas con la enfermedad que se estudia, y los controles deben obtenerse de la población de donde surgieron los casos, para evitar sesgos de selección, los cuales podrían invalidar los resultados

Figura 5. Esquemas conceptuales de diseño y análisis para un estudio de casos y controles

En un estudio de casos y controles, los marginales de las columnas están fijos porque el investigador decide qué relación desea, la mínima es 1 caso × 1 control, pero en general se señala que la relación 1 caso × 4 controles es con la que se alcanza la mayor información. El objetivo de aumentar la razón caso/control es obtener un mayor poder estadístico. Esta medida se obtiene mediante la siguiente ecuación:

2. Riesgo relativo

Si se analiza la incidencia acumulada se obtiene la razón de riesgos y si se estudia la DI se calcula la razón de tasas. En forma general, ambas se conocen como riesgo relativo (RR), pero depende del tipo de incidencia que se estudie. Estas medidas se obtienen de un estudio de cohorte (Figura 6), en el que se examinan dos grupos de población sin enfermedad, uno expuesto y otro no al factor de estudio. Ambas cohortes se siguen durante un tiempo específico y se observa a los enfermos que se presentan en una y otra. Los marginales de los renglones de la tabla cuadricelular son fijos porque el investigador calcula el número de expuestos y no expuestos que debe estudiar para responder la hipótesis planteada.

Figura 6. Esquemas conceptuales de diseño y análisis para un estudio de cohorte

La razón de riesgos y la razón de tasas se estiman con la siguiente fórmula, en la cual lo único que cambia es el tipo de incidencia (IA o DI):

Medidas de impacto potencial

Las medidas de impacto potencial evalúan la efectividad que tienen las acciones realizadas por el personal de salud en el control de las enfermedades. Es decir, cuando se conoce uno o varios factores de riesgo asociados a una enfermedad y es posible eliminarlos, estas medidas indican cuánta proporción de enfermedad podrá evitarse al quitar el o los factores involucrados en la causalidad. En general se conocen 3 medidas de impacto potencial:

• Riesgo atribuible o diferencia de riesgo
• Fracción etiológica de expuestos
• Fracción etiológica poblacional
• Riesgo atribuible o diferencia de riesgos

La diferencia de riesgos (o riesgo atribuible) fue la primera medida de impacto potencial que se conoció y consiste solo en restar al riesgo en expuestos, el riesgo en no expuestos y, posteriormente, el resultado se multiplica por 100. El resultado será la proporción de enfermedad que podrá disminuirse al eliminar el factor de riesgo:

Donde:

DR = diferencia de riesgo

Una de las limitaciones de esta medición es que solo puede utilizarse cuando se estima alguna medida de frecuencia, sea prevalencia (en un estudio transversal analítico) o la incidencia (en un estudio de cohorte); por ello en los estudios de casos y controles no podrá estimarse porque no es posible calcular medidas de frecuencia en este diseño. El otro problema es que puede subestimar la proporción de riesgo. Por lo tanto, surgieron otras medidas de impacto potencial: la fracción etiológica en expuestos y la fracción etiológica poblacional, las cuales no tienen las limitaciones señaladas del riesgo atribuible.

Fracciones etiológicas en un estudio transversal analítico

Fracción etiológica en expuestos:

Donde:

FE_e = fracción etiológica en expuestos;

RP = razón de prevalencias

Fracción etiológica poblacional:

Donde:

FE_p= fracción etiológica poblacional

RP = razón de prevalencias

Fracciones etiológicas en un estudio de casos y controles

Fracción etiológica en expuestos:

Donde:

FE_e = Fracción etiológica en expuestos;

RM = Razón de momios

Fracción etiológica poblacional:

Donde:

FE_p= fracción etiológica poblacional

RM = razón de momios

Fracciones etiológicas en un estudio de cohorte

Fracción etiológica en expuestos:

Donde:

FE_e = fracción etiológica en expuestos;

RR = razón de riesgos o de tasas dependiendo del tipo de incidencia que se calcule

Fracción etiológica poblacional:

Donde:

FE_p = fracción etiológica poblacional;

RR = razón de riesgos o de tasas dependiendo el tipo de incidencia que se calcule

Síntesis y conclusiones

En el Cuadro 2 se sintetizan las medidas de frecuencia, de asociación o impacto potencial que pueden calcularse según el tipo de estudio.

Hay que considerar que las medidas para describir poblaciones tienen que ser interpretadas apropiadamente para que sean utilizadas a fin de tomar decisiones en diferentes escenarios, ya sea directamente en pacientes, hospitales, estados o países. Además, potencialmente deberán servir para llevar a cabo estudios de investigación para determinar, en su caso, alguna etiología y con ello ayudar a disminuir el riesgo de morbilidad o mortalidad de una población determinada.

Se espera que la síntesis de las diferentes medidas de la epidemiología descriptiva y de la epidemiología analítica que se presentan en este artículo de revisión, sirva de apoyo para que tanto la prevalencia, incidencia, el riesgo relativo, razón de momios, o bien, las medidas de impacto sean obtenidas de una manera más eficiente y, que su conocimiento ayude a tomar mejores decisiones clínicas.

Agradecimientos

Se agradece al doctor Miguel Ángel Villasís Keever su apoyo en la revisión y edición del artículo, así como por la traducción del resumen al idioma Inglés.

Bibliografía

1. Abramson JH. Making sense of data. Segunda edición. New York, USA: Oxford University Press; 1994.
2. Argimon JP, Jiménez JV. Métodos de investigación clínica y epidemiológica. Tercera edición. Madrid, España: Elsevier España; 2004.
3. Fajardo-Gutiérrez A, Rendón-Macías ME, Mejía-Aranguré JM. Epidemiología del cáncer en niños mexicanos. Resultados globales. Rev Med Inst Mex Seguro Soc. 2011;49(Supl 1):S43-S70.
4. Greemberg RS, Daniels SR, Flanders WD, Eley JW, Boring JR. Medical epidemiology. Tercera edición. New York, USA: McGraw-Hill; 2001.
5. Hospital Universitario Ramón y Cajal. [Sitio web]. Material docente de la Unidad de Bioestadística Clínica. Abraira V. Medidas de frecuencia de la enfermedad. Disponible en: http://www.hrc.es/bioest/Medidas_frecuencia_1.html
6. Kleinbaum, D G, Kupper LL, Morgenstern H. Epidemiologic research, principles and quantitative methods. Belmont, CA, USA: Lifetime Learning Publications; 1982.
7. Last JM. A Dictionary of epidemiology. Cuarta edición. New York, USA: Oxford University Press; 2001.
8. Lordoño JLF. Metodología de la investigación epidemiológica. Tercera edición. Bogotá, Colombia: El Manuel Moderno; 2004.

Recibido: 2016-12-21

Aceptado: 2017-01-05

Correspondencia: Arturo Fajardo-Gutiérrez. afajardo@unam.mx

Todo el contenido de esta revista, excepto dónde está identificado, está bajo una Licencia Creative Commons

revistaalergia.mx